|
|
什么是无限 Infinity?很多人都说我们见到的宇宙是无限大,至今时间是无限长,有无限智慧等,这都是扯谈!
Google名字来源~=googol=10^100>10^80~=可观测到宇宙所有原子!
Google总部名字~=googolplex=10^googol= 10^(10^100)。
如果整个可观测到宇宙装满了1.5微米大小的灰尘颗粒,那么这些颗粒不同的组合和数量~=googolplex。
但吉尼斯记录最大数字用在数学证明是Graham的数字。
懂英文的可以看看下面的英文视频和文章关于Graham的数字,虽然Graham的数字的googolplex分之一已经是巨大无比,可想Graham的数字是无可意义的巨大,但还是没到 无限Infinity!
http://emptv.com/videos/a-taste-of-infinity
http://io9.com/5807256/whats-the-biggest-number-in-the-universe
These are the biggest numbers in the universe

There are numbers out there that are so enormously, impossibly vast that to even write them down would require the entire universe. But here's the really crazy thing...some of these incomprehensibly huge numbers are crucial for understanding the world.
When I say "the biggest number in the universe", what I really mean is the biggestmeaningful number, the largest possible number that is in some way useful. There are lots of contenders for this title, but I'll warn you now: there is a very real risk that trying to understand all this will blow your mind. But then, with extreme math, that's half the fun. Googol and GoogolplexWe might as well begin with what are quite probably the two largest numbers you've ever heard of, and are in fact the two largest numbers with commonly accepted definitions in the English language. (There's a fairly robust nomenclature available for naming numbers as high as you want to go, but you won't find these in dictionaries at the present time.) The googol, which has since become world famous (albeit misspelled) in the form of Google, began life in 1920 as a way to get children interested in large numbers. To that end, mathematician Edward Kasner (pictured) took his two nephews, Milton and Edwin Sirotta, on a walk through the New Jersey Palisades. He asked them for any ideas they might have, and the then nine-year-old Milton proposed "googol." Where he got this particular word is unknown, but Kasner decided that 10^100 - or, the number one followed by a hundred zeroes - would henceforth be known as a googol. But young Milton wasn't finished - he also proposed an even larger number, the googolplex. This number, according to Milton, was 1 followed by as many zeroes as you could write before you got tired. Though a charming idea, Kasner decided a more technical definition was needed. As he explained in his 1940 book Mathematics and the Imagination, Milton's definition left open the dicey possibility that a random buffoon could become a greater mathematician than Albert Einstein simply by possessing greater endurance. So, Kasner decided a googolplex would be 10^googol, or 1 followed by a googol of zeroes. To put that another way - and in similar notation to how we'll be dealing with various other numbers we'll be talking about - a googolplex is 10^10^100. To put that in some mindbending perspective, Carl Sagan once pointed out that it would physically impossible to write down all the zeroes in a googolplex, because there simply isn't enough room in the universe. If you filled the entire volume of the observable universe with fine dust particles roughly 1.5 micrometers in size, then the number of different combinations in which you could arrange and number these particles would be about one googolplex. Linguistically speaking, googol and googolplex are probably the two biggest meaningful numbers (at least in English), but as we're about to find out, there's no end of ways to define "meaningful." The Real WorldIf we're going to talk about the largestmeaningful number, there's a not terrible argument that that really means we need to find the largest number with any real world significance. We can start the bidding with the current human population, which is currently about 6.92 billion. The global economy in 2010 is estimated to have been about $61.96 trillion, but both of those are dwarfed by the roughly 100 quadrillion cells that make up the human body. Of course, none of these can compare to the total number of particles in the universe, which is generally thought to be around 10^80 - a number so large that our language doesn't have an agreed upon word for it. We can play around a bit with measurements as we get larger and larger - for instance, the weight of the Sun in tons will produce a smaller value than if you measure it in pounds. The fairest way to do this is to use the Planck units, which are the smallest possible measurements for which the laws of physics still hold. For instance, the age of the universe in Planck time is about 8 * 10^60. If we go right back to the first unit of Planck time after the Big Bang, we find the density of the universe was 5.1 * 10^96. We're getting bigger, but we still haven't even reached a googol.
How Many Universes Exist in the Multiverse? Physicists May Have a Number
If we do, in fact, live in a multiverse, with multiple universes arising out of the Big Bang, how many are there? Andrei Linde and Vitaly Vanchurin… Read…
The largest number with any real world application - or, in this case, real worldsapplication - is probably 10^10^10^7, which is one recent estimate of the number of universes in the multiverse. That number is so huge that the human brain would be literally unable to perceive all those different universes, as the mind is only capable of roughly 10^10^16 configurations. Actually, that number is probably the biggest with any practical application, assuming you don't buy into the whole multiverse idea. But there are still far larger numbers lurking out there. But in order to find them, we're going to need to venture in the realm of pure mathematics, and there's no better place to start than with the prime numbers. The Mersenne PrimesPart of the difficulty here is coming up with a good definition for what a "meaningful" number actually is. One way to think about is in terms of prime and composite numbers. A prime number, as you probably remember from high school math, is any number whose only divisors are 1 and itself. So, 2, 3, and 5 are all prime numbers, while 4 (2*2) and 6 (2*3) are both composite numbers. This means that any composite number can ultimately be reduced to its prime divisors. In a sense, a number like 5 is more important than, say, 4 because there's no way to express it in terms of smaller numbers. Obviously, we can extend this quite a bit further. 100, for instance, is really just 2*2*5*5, which means that in a hypothetical world where our knowledge of numbers only went up to 5, mathematicians could still express the number 100. But the very next number101 is prime, which means the only way to express it is to have direct knowledge of its existence. This means that the largest known prime numbers are important in a way that, say, a googol - which is ultimately just a bunch of 2's and 5's multiplied together - really isn't. And, because prime numbers are essentially random, there's no known way to predict what impossibly large number will actually be prime. To this day, a discovery of a new prime number is a big deal.  Ancient Greek mathematicians understood the concept of prime numbers at least as far back as 500 BCE, but 2000 years later people still only knew which numbers were prime up to about 750. Thinkers as far back as Euclid saw a potential shortcut, but it wouldn't be until the Renaissance that mathematicians could really put this in practice. These are known as the Mersenne numbers, named after 17th century French scholar Marin Mersenne. The idea is simple enough: a Mersenne prime is any number of the form 2^n-1. So, for instance, 2^2 - 1 = 4 - 1 = 3, which is prime, and the same is true for 2^5 - 1 = 32 - 1 = 31. It's much quicker and easier to identify Mersenne primes than any other type of prime, and computers have been hard at work looking for them for the past six decades. Until 1952, the largest known prime number was 2^127 - 1, a number with 39 digits. That year, computers determined that 2^521 - 1 is prime, and that number has 157 digits, which already makes it far bigger than a googol. Computers have been on the hunt ever since, and currently the 47th Mersenne prime is the largest known to humanity. Discovered in 2008, it is 2^43,112,609 - 1, which is a number with nearly 13 million digits. That's the largest known number that can't be expressed in terms of any smaller numbers - although if you want to help find an even bigger Mersenne prime, you (and your computer) are always welcome to join the search. Skewes' NumberLet's stay with the prime numbers for a second. As I said before, the primes are fundamentally irregular, which means there's no way to predict what the next prime will be. Mathematicians have had to go to some pretty fantastic lengths to come up with any way to predict future primes in even the vaguest of senses. The most successful of these attempts is probably the prime-counting function, which the legendary mathematician Carl Friedrich Gauss came up with in the late 1700s. I'll spare you the more complex math - we've got plenty still to come anyway - but the gist of the function is this: for any given integer x, it's possible to estimate how many prime numbers there are that are smaller than x. For instance, if x = 1,000, the function predicts that there should be 178 prime numbers; if x = 10,000, there are 1,246 primes smaller than it; and if x = 1,000,000, then there are 78,628 smaller numbers that are prime. Here's the thing though - prime numbers really are irregular, and so this is just a close approximation of the actual number of primes. In reality, we know that there are 168 primes smaller than 1,000, 1,229 primes smaller than 10,000, and 78,498 primes smaller than 1,000,000. It's an excellent estimate, to be sure, but it's always just an estimate...and, more specifically, an overestimate. In all known cases up to about 10^22, the prime-counting function slightly overestimates the actual number of primes smaller than x. Mathematicians once thought that this would be the case all the way up to infinity - it certainly holds true for some unimaginably huge quantities - but in 1914 John Edensor Littlewood proved that, at some unknown, incomprehensibly vast figure, the prime-counting function would start providing an underestimate of the number of primes, and then the function would switch back between over- and underestimates an infinite number of times.  The hunt was on for the crossover point, and that's where Stanley Skewes (pictured) makes his entrance. In 1933, he proved that the upper bound for when the prime-counting function first becomes an understimate is 10^10^10^34. It's hard to really comprehend in even the most abstract sense what a number like that actually is, and to that point it was easily the largest number ever used in a serious mathematical proof. Since then, mathematicians have been able to reduce the upper limit to the relatively tiny figure of about 10^316, but the original figure remains known as Skewes' number. So just how big is 10^10^10^34, a number that dwarfs even the mighty googolplex? In The Penguin Dictionary of Curious and Interesting Numbers, David Wells relates one way in which mathematician G.H. Hardy managed to conceptualize the size of Skewes' Number: Hardy thought it 'the largest number which has ever served any definite purpose in mathematics', and suggested that if a game of chess was played with all the particles in the universe as pieces, one move being the interchange of a pair of particles, and the game terminating when the same position recurred for the 3rd time, the number of possible games would be about Skewes' number.
One last thing before we move on: the Skewes' number we've been talking about is the smallerof the two. There's another Skewes' number that the mathematician demonstrated in 1955. The first number relies on something called the Riemann hypothesis being true - it's a particularly complex bit of mathematics that remains unproven but is massively helpful when it comes to prime numbers. Still, if the Riemann hypothesis is false, Skewes found that the crossover point jumps all the way up to 10^10^10^963. A Matter of MagnitudeBefore we get to the number that makes even Skewes' number look tiny, we need to talk a little bit about scale, because otherwise there's really no way to appreciate where we're about to go. Let's first look at the number 3 - it's a tiny number, so small that humans can actually have an intuitive understanding of what it means. There are very few numbers that fit that description, as anything beyond about six stops being a distinct number and starts being "several", "many", and so on. Now, let's look at 3^3, which is 27. While we can't really intuitively understand what 27 is in the same way that we can for 3, it's perfectly easy to visualize what 27 of something is. So far, so good. But what if we go on to 3^3^3? That's equal to 3^27, or 7,625,597,484,987. We're well past the point of being able to visualize that amount as anything other than a generically large number - we lose the ability to comprehend the individual parts somewhere around a million. (Admittedly, it would take an insanely long amount of time to actually count a million of anything, but the point is that we're still able to perceive it.) Even so, while we can't visualize what 3^3^3 is, we're at least able to understand in broad terms what 7.6 trillion is, perhaps by comparing it to something like the US's GDP. We've moved from intuition to visualization to mere understanding, but at least we still have some grasp on what the number is. That's about to change, as we move another rung up the ladder. For this, we'll need to switch to a notation invented by Donald E. Knuth, known as up-arrow notation. In this notation, 3^3^3 can be rewritten as 3^^3. When we then move to 3^^^3, the value that we're talking about is equal to 3^^(3^^3). This is equal to 3^3^3^...^3^3^3, where there are a total of 7,625,597,484,987 terms. We've now well and truly blasted past all the other numbers we've discussed. After all, even the biggest of those had just three or four terms in the exponential series. For instance, even the super-Skewes' number was "just" 10^10^10^963 - even adjusting for the fact that those are all much larger numbers than 3, it's still absolutely nothing compared to an exponent tower with 7.6 trillion terms. Obviously, there's no way to even begin to comprehend a number so huge...and yet, the processby which it's created can still be understood. We might not be able to grasp the actual numberthat is produced by an exponent tower with 7.6 trillion 3's in it, but we can basically visualize an exponent tower with that many terms in it, and indeed a decent supercomputer would be able to store the tower, even if it couldn't begin to calculate its actual value. This is getting increasingly abstract, but it's only going to get worse. You might think that 3^^^^3 is an exponent tower of 3's that is 3^^^3 long (indeed, in a previous version of this post, I made precisely that mistake), but that is just 3^^^4. In other words, imagine you had the ability to calculate the precise value of an exponential tower of 3's that was 7,625,597,484,987 terms long, and then you took that value and created a new tower with that many 3's in it...that gets you 3^^^4. Repeating that process with each successive number until you've done it 3^^^3 times will, at last, get you to 3^^^^3. This is a number that is just incomprehensibly vast, but at least the steps involved can still sort of be grasped, if we take things very slowly. We can no longer understand the number or visualize the procedure that would create it, but at least we can understand the basic procedure, if only in the vaguest possible terms. Now prepare for your mind to be really blown. Graham's NumberHere's how you get to Graham's number, which holds a place in the Guinness Book of World Records as the largest number ever used in a mathematical proof. It's utterly impossible to imagine how vast Graham's number is, and it honestly isn't much easier to explain exactly what it is. Basically, Graham's number comes into play when dealing with hypercubes, which is a theoretical geometric shape with more than three dimensions. Mathematician Ronald Graham (pictured, awesomely) wanted to figure out what would be the smallest number of dimensions needed for certain properties of the hypercube to remain stable. (Sorry to be so vague in explaining this, but I'm pretty sure we'd all need to get at least two graduate degrees in mathematics before we get any more specific.) In any event, Graham's number is the upper limit for this minimum number of dimensions. And just how big is this particular upper bound? Well, let's go back to 3^^^^3, a number so larger that we can only understand the procedure behind it in the vaguest of senses. Now, instead of simply jumping up one more level to 3^^^^^3, we're going to consider the number 3^^....^^3, in which there are 3^^^^3 arrows between those two threes. At this point, we're far beyond even the tiniest possible comprehension of what a number like this is, or even how you would go about calculating it. Now repeat that process 62 more times. That, ladies and gentlemen, is Graham's number, a number that is about 64 orders of magnitude past the point of human comprehension. This is a number that is so much greater than any number you could possibly imagine - hell, it's much larger than any infinity that you could ever hope to imagine - that it simply defies even the most abstract of descriptions. But here's the weird thing. Because Graham's number is basically just a bunch of 3's multiplied together, that means that we can know some of its properties without actually calculating the whole thing. We can't represent Graham's number with any familiar notation - even if we used the entire universe to write it down - but I can tell you right now what the last twelve digits of Graham's Number are: 262,464,195,387. And that's nothing - we know at least the last 500 digits of Graham's number. Of course, it's worth remembering that this number is just an upper limit for Graham's original problem. It's possible that the actual number of dimensions that you need for the properties to hold is much, much smaller. In fact, back in the 1980s, the considered opinion of most experts in this area was that the actual answer was just six - a number so tiny that we can understand it on an intuitive level. Since then, the lower limit has been raised to 13, but there's still a very good chance that the actual solution to Graham's problem isn't anywhere near as big as Graham's number. Towards InfinitySo, are there numbers even bigger than Graham's number? Well, of course there are - there's Graham's number + 1, for a start. As for meaningful numbers...well, there are some fiendishly complicated areas of math (particularly an area known as combinatorics) and computer science that do feature numbers even bigger than Graham's number. But we've pretty much reached the limit of what I could ever hope to sensibly explain. For those foolhardy enough to delve still further, you can check out some of the additional reading at your own peril. And yet, there's still something even bigger out there, something so big that the term ceases to have all meaning: infinity. So join us next week for part two of our odyssey into the largest numbers imaginable, as we examine all the many flavors of infinity. Until then, I leave you with this amazing quote attributed to Douglas Reay: I have this vision of hoards of shadowy numbers lurking out there in the dark, beyond the small sphere of light cast by the candle of reason. They are whispering to each other; plotting who knows what. Perhaps they don't like us very much for capturing their smaller brethren with our minds. Or perhaps they just live uniquely numberish lifestyles, out there beyond our ken.
Further Reading
http://en.wikipedia.org/wiki/Knuth%27s_up-arrow_notation
Knuth's up-arrow notation
Introduction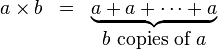 For example,  Exponentiation for a natural power  is defined as iterated multiplication, which Knuth denoted by a single up-arrow:  For example,  To extend the sequence of operations beyond exponentiation, Knuth defined a “double arrow” operator to denote iterated exponentiation ( tetration):  For example,  Here and below evaluation is to take place from right to left, as Knuth's arrow operators (just like exponentiation) are defined to be right-associative. According to this definition,  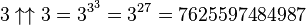  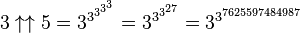 etc. etc.This already leads to some fairly large numbers, but Knuth extended the notation. He went on to define a “triple arrow” operator for iterated application of the “double arrow” operator (also known as pentation):  followed by a 'quadruple arrow' operator (also known as hexation):  and so on. The general rule is that an  -arrow operator expands into a right-associative series of ( 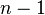 )-arrow operators. Symbolically,  Examples:   The notation  is commonly used to denote  with n arrows.
NotationIn expressions such as  , the notation for exponentiation is usually to write the exponent  as a superscript to the base number  . But many environments — such as programming languages and plain-text e-mail — do not support superscript typesetting. People have adopted the linear notation  for such environments; the up-arrow suggests 'raising to the power of'. If the character set doesn't contain an up arrow, the caret ^ is used instead. The superscript notation  doesn't lend itself well to generalization, which explains why Knuth chose to work from the inline notation  instead.  is a shorter alternative notation for n uparrows. Thus  . Attempting to write  using the familiar superscript notation gives a power tower.  If b is a variable (or is too large), the power tower might be written using dots and a note indicating the height of the tower.  Continuing with this notation,  could be written with a stack of such power towers, each describing the size of the one above it.  Again, if b is a variable or is too large, the stack might be written using dots and a note indicating its height.  Furthermore, 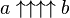 might be written using several columns of such stacks of power towers, each column describing the number of power towers in the stack to its left:  And more generally:  This might be carried out indefinitely to represent  as iterated exponentiation of iterated exponentiation for any a, n and b (although it clearly becomes rather cumbersome). The tetration notation  allows us to make these diagrams slightly simpler while still employing a geometric representation (we could call these tetration towers).    Finally, as an example, the fourth Ackermann number  could be represented as: 
GeneralizationsSome numbers are so large that multiple arrows of Knuth's up-arrow notation become too cumbersome; then an n-arrow operator  is useful (and also for descriptions with a variable number of arrows), or equivalently, hyper operators. Some numbers are so large that even that notation is not sufficient. Graham's number is an example. The Conway chained arrow notation can then be used: a chain of three elements is equivalent with the other notations, but a chain of four or more is even more powerful.  It is generally suggested that Knuth's arrow should be used for smaller magnitude numbers, and the chained arrow or hyper operators for larger ones. Definition[edit source | editbeta]The up-arrow notation is formally defined by  for all integers  with  . All up-arrow operators (including normal exponentiation,  ) are right associative, i.e. evaluation is to take place from right to left in an expression that contains two or more such operators. For example,  , not  ; for example
 is  not  There is good reason for the choice of this right-to-left order of evaluation. If we used left-to-right evaluation, then  would equal  , so that  would not be an essentially new operation. Right associativity is also natural because we can rewrite the iterated arrow expression  that appears in the expansion of  as  , so that all the  s appear as left operands of arrow operators. This is significant since the arrow operators are not commutative. The definition could be extrapolated one step, starting with  if n = 0, because exponentiation is repeated multiplication starting with 1. Extrapolating one step more, writing multiplication as repeated addition, is not as straightforward because multiplication is repeated addition starting with 0 instead of 1. "Extrapolating" again one step more, writing addition of n as repeated addition of 1, requires starting with the number a. Compare the definition of the hyper operator, where the starting values for addition and multiplication are also separately specified.
Tables of values
Computing 2↑mnComputing  can be restated in terms of an infinite table. We place the numbers 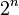 in the top row, and fill the left column with values 2. To determine a number in the table, take the number immediately to the left, then look up the required number in the previous row, at the position given by the number just taken.  = hyper(2, m + 2, n) = 2 → n → m = hyper(2, m + 2, n) = 2 → n → mm\n | 1 | 2 | 3 | 4 | 5 | 6 | formula | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 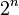 | 2 | 2 | 4 | 16 | 65536 |  |  | 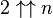 | 3 | 2 | 4 | 65536 |  | | |  | 4 | 2 | 4 |  | | | |  |
Computing 3↑mn[edit source | editbeta]We place the numbers  in the top row, and fill the left column with values 3. To determine a number in the table, take the number immediately to the left, then look up the required number in the previous row, at the position given by the number just taken.  = hyper(3, m + 2, n) = 3 → n → m = hyper(3, m + 2, n) = 3 → n → mm\n | 1 | 2 | 3 | 4 | 5 | formula | 1 | 3 | 9 | 27 | 81 | 243 |  | 2 | 3 | 27 | 7,625,597,484,987 |  | |  | 3 | 3 | 7,625,597,484,987 |  | | |  | 4 | 3 |  | | | |  |
Computing 10↑mnWe place the numbers 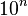 in the top row, and fill the left column with values 10. To determine a number in the table, take the number immediately to the left, then look up the required number in the previous row, at the position given by the number just taken.  = hyper(10, m + 2, n) = 10 → n → m = hyper(10, m + 2, n) = 10 → n → mm\n | 1 | 2 | 3 | 4 | 5 | formula | 1 | 10 | 100 | 1,000 | 10,000 | 100,000 | 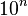 | 2 | 10 | 10,000,000,000 | 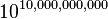 |  |  |  | 3 | 10 |  |  |  | |  | 4 | 10 |  |  | | |  |
Note that for 2 ≤ n ≤ 9 the numerical order of the numbers  is the lexicographical order with m as the most significant number, so for the numbers of these 8 columns the numerical order is simply line-by-line. The same applies for the numbers in the 97 columns with 3 ≤ n ≤ 99, and if we start from m = 1 even for 3 ≤ n ≤ 9,999,999,999. R. L. Goodstein, [2] with a system of notation different from Knuth arrows, used the sequence of hyperoperators here denoted by  to create systems of numeration for the nonnegative integers. Letting superscripts  denote the respective hyperoperators  , the so-called complete hereditary representation of integer n, at level k and base b, can be expressed as follows using only the first k hyperoperators and using as digits only 0, 1, ..., b-1: - For 0 ≤ n ≤ b-1, n is represented simply by the corresponding digit.
- For n > b-1, the representation of n is found recursively, first representing n in the form
 where xk, ..., x1 are the largest integers satisfying (in turn) where xk, ..., x1 are the largest integers satisfying (in turn) 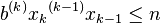 ... ... .Any xi exceeding b-1 is then re-expressed in the same manner, and so on, repeating this procedure until the resulting form contains only the digits 0, 1, ..., b-1. .Any xi exceeding b-1 is then re-expressed in the same manner, and so on, repeating this procedure until the resulting form contains only the digits 0, 1, ..., b-1.The remainder of this section will use  , rather than superscripts, to denote the hyperoperators. Unnecessary parentheses can be avoided by giving higher-level operators higher precedence in the order of evaluation; thus, level-1 representations have the form  , with X also of this form; level-2 representations have the form  , with X, Y also of this form; level-3 representations have the form  , with X, Y, Z also of this form; level-4 representations have the form  , with X, Y, Z, T also of this form; and so on. The representations can be abbreviated by omitting any instances of  etc.; for example, the level-3 base-2 representation of the number 6 is  , which abbreviates to  . Examples: The unique base-2 representations of the number 266, at levels 1, 2, 3, 4, and 5 are as follows:  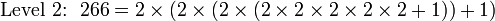    . .
See alsoReferences
http://en.wikipedia.org/wiki/Graham's_number
Graham's number
This article is about the large number named after Ronald Graham. For the investing term named after Benjamin Graham, see Graham number.
The number gained a degree of popular attention when Martin Gardner described it in the "Mathematical Games" section of Scientific American in November 1977, writing that, "In an unpublished proof, Graham has recently established ... a bound so vast that it holds the record for the largest number ever used in a serious mathematical proof." The 1980 Guinness Book of World Records repeated Gardner's claim, adding to the popular interest in this number. According to physicist John Baez, Graham invented the quantity now known as Graham's number in conversation with Gardner himself. While Graham was trying to explain a result in Ramsey theory which he had derived with his collaborator B. L. Rothschild, Graham found that the quantity now known as Graham's number was easier to explain than the actual number appearing in the proof. Because the number which Graham described to Gardner is larger than the number in the paper itself, both are valid upper bounds for the solution to the Ramsey-theory problem studied by Graham and Rothschild. [1]Specific integers known to be far larger than Graham's number have since appeared in many serious mathematical proofs (e.g., in connection with Friedman's various finite forms of Kruskal's theorem).
Context 
Example of a 2-colored 3-dimensional cube containing one single-coloured 4-vertex coplanar complete subgraph. The subgraph is shown below the cube. Note that this cube would contain no such subgraph if, for example, the bottom edge in the present subgraph were replaced by a blue edge – thus proving by counterexample that N* > 3.
Graham's number is connected to the following problem in Ramsey theory: Connect each pair of geometric vertices of an n-dimensional hypercube to obtain a complete graph on 2 n vertices. Colour each of the edges of this graph either red or blue. What is the smallest value of n for which every such colouring contains at least one single-coloured complete subgraph on four coplanar vertices?
In 1971, Graham and Rothschild proved that this problem has a solution N*, giving as a bound 6 ≤ N* ≤ N, with N being a large but explicitly defined number 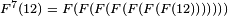 , where  in Knuth's up-arrow notation; the number is between 4 → 2 → 8 → 2 and 2 → 3 → 9 → 2 in Conway chained arrow notation. [2] This was reduced in 2013 via upper bounds on the Hales–Jewett number to  . [3] The lower bound of 6 was later improved to 11 by Geoff Exoo in 2003, and to 13 by Jerome Barkley in 2008. Thus, the best known bounds for N* are 13 ≤ N* ≤ N'. Graham's number, G, is much larger than N:  , where  . This weaker upper bound for the problem, attributed to an unpublished work of Graham, was eventually published and named by Martin Gardner in Scientific American in November 1977. [4]
Definition where the number of arrows in each layer, starting at the top layer, is specified by the value of the next layer below it; that is, 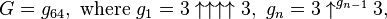 and where a superscript on an up-arrow indicates how many arrows there are. In other words, G is calculated in 64 steps: the first step is to calculate g1 with four up-arrows between 3s; the second step is to calculate g2 with g1 up-arrows between 3s; the third step is to calculate g3 with g2 up-arrows between 3s; and so on, until finally calculating G = g64 with g63 up-arrows between 3s. Equivalently,   Magnitude[edit source | editbeta] Magnitude[edit source | editbeta]To convey the difficulty of appreciating the enormous size of Graham's number, it may be helpful to express—in terms of exponentiation alone—just the first term ( g1) of the rapidly growing 64-term sequence. First, in terms of tetration (  ) alone: 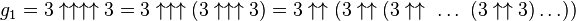 where the number of 3s in the expression on the right is  Now each tetration (  ) operation reduces to a "tower" of exponentiations (  ) according to the definition  Thus,  becomes, solely in terms of repeated "exponentiation towers",  and where the number of 3s in each tower, starting from the leftmost tower, is specified by the value of the next tower to the right. In other words, g1 is computed by first calculating the number of towers, n = 3↑3↑3↑...↑3 (where the number of 3s is 3↑3↑3 = 7625597484987), and then computing the nthtower in the following sequence: 1st tower: 3 2nd tower: 3↑3↑3 (number of 3s is 3) = 7625597484987 3rd tower: 3↑3↑3↑3↑...↑3 (number of 3s is 7625597484987) = … ⋮ g1 = nth tower: 3↑3↑3↑3↑3↑3↑3↑...↑3 (number of 3s is given by the n-1th tower)where the number of 3s in each successive tower is given by the tower just before it. Note that the result of calculating the third tower is the value of n, the number of towers forg1. The magnitude of this first term, g1, is so large that it is practically incomprehensible, even though the above display is relatively easy to comprehend. Even n, the mere number of towers in this formula for g1, is far greater than the number of Planck volumes (roughly 10185 of them) into which one can imagine subdividing the observable universe. And after this first term, still another 63 terms remain in the rapidly growing g sequence before Graham's number G = g64 is reached. Graham's number is a "power tower" of the form 3↑↑n (with a very large value of n), so its rightmost decimal digits must satisfy certain properties common to all such towers. One of these properties is that all such towers of height greater than d (say), have the same sequence of d rightmost decimal digits. This is a special case of a more general property: The d rightmost decimal digits of all such towers of height greater than d+2, are independent of the topmost "3" in the tower; i.e., the topmost "3" can be changed to any other nonnegative integer without affecting the d rightmost digits. The following table illustrates, for a few values of d, how this happens. For a given height of tower and number of digits d, the full range of d-digit numbers (10d of them) does notoccur; instead, a certain smaller subset of values repeats itself in a cycle. The length of the cycle and some of the values (in parentheses) are shown in each cell of this table: Number of different possible values of 3↑3↑…3↑x when all but the rightmost d decimal digits are ignored
| Number of digits (d) | 3↑x | 3↑3↑x | 3↑3↑3↑x | 3↑3↑3↑3↑x | 3↑3↑3↑3↑3↑x | | 1 | 4
(1,3,9,7) | 2
(3,7) | 1
(7) | 1
(7) | 1
(7) | | 2 | 20
(01,03,…,87,…,67) | 4
(03,27,83,87) | 2
(27,87) | 1
(87) | 1
(87) | | 3 | 100
(001,003,…,387,…,667) | 20
(003,027,…387,…,587) | 4
(027,987,227,387) | 2
(987,387) | 1
(387) |
The particular rightmost d digits that are ultimately shared by all sufficiently tall towers of 3s are in bold text, and can be seen developing as the tower height increases. For any fixed number of digits d (row in the table), the number of values possible for 3  3↑…3↑ x mod 10 d, as x ranges over all nonnegative integers, is seen to decrease steadily as the height increases, until eventually reducing the "possibility set" to a single number (colored cells) when the height exceeds d+2. A simple algorithm [5] for computing these digits may be described as follows: let x = 3, then iterate, d times, the assignment x = 3 x mod 10 d. Except for omitting any leading 0s, the final value assigned to x (as a base-ten numeral) is then composed of the d rightmost decimal digits of 3↑↑ n, for all n > d. (If the final value of x has fewer than d digits, then the required number of leading 0s must be added.) Let k be the numerousness of these stable digits, which satisfy the congruence relation G(mod 10k)≡[GG](mod 10k). k= t-1, where G( t):=3↑↑ t. [6] It follows that, g63 ≪ k ≪ g64. The algorithm above produces the following 500 rightmost decimal digits of Graham's number (or of any tower of more than 500 3s): …02425950695064738395657479136519351798334535362521 43003540126026771622672160419810652263169355188780 38814483140652526168785095552646051071172000997092 91249544378887496062882911725063001303622934916080 25459461494578871427832350829242102091825896753560 43086993801689249889268099510169055919951195027887 17830837018340236474548882222161573228010132974509 27344594504343300901096928025352751833289884461508 94042482650181938515625357963996189939679054966380 03222348723967018485186439059104575627262464195387
See alsoNotes
References- Graham, R. L.; Rothschild, B. L. (1971). "Ramsey's Theorem for n-Parameter Sets". Transactions of the American Mathematical Society 159: 257–292.doi:10.2307/1996010. JSTOR 1996010. The explicit formula for N appears on p. 290. This is not the "Graham's number" G published by Martin Gardner.
- Graham, R. L.; Rothschild, B.L. (1978). "Ramsey Theory", Studies in Combinatorics, Rota, G.-G., ed., Mathematical Association of America, 17:80–99. On p. 90, in stating "the best available estimate" for the solution, the explicit formula for N is repeated from the 1971 paper.
- Gardner, Martin (November 1977). "Mathematical Games". Scientific American 237: 18–28.; reprinted (revised) in Gardner (2001), cited below.
- Gardner, Martin (1989). Penrose Tiles to Trapdoor Ciphers. Washington, D.C.: Mathematical Association of America. ISBN 0-88385-521-6.
- Gardner, Martin (2001). The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems. New York, NY: Norton. ISBN 0-393-02023-1.
- Exoo, Geoffrey (2003). "A Euclidean Ramsey Problem". Discrete and Computational Geometry 29 (2): 223–227. doi:10.1007/s00454-002-0780-5. Exoo refers to the Graham & Rothschild upper bound N by the term "Graham's number". This is not the "Graham's number" G published by Martin Gardner.
- Barkley, Jerome (2008). "Improved lower bound on an Euclidean Ramsey problem". arXiv:0811.1055v1 [math.CO].
External links[edit source | editbeta]
|
本帖子中包含更多资源
您需要 登录 才可以下载或查看,没有帐号?立即注册

x
|